การตั้งเป้าหมายการเงิน ไม่ว่าจะเป็นการลงทุนในหุ้น กองทุน หรือการเก็บออมโดยฝากเงินไว้ในบัญชีเงินฝากดิจิทัล หรือบัญชีเงินฝากประจำ ทุกคนต่างก็มีวัตถุประสงค์ที่จะได้ผลตอบแทนที่เพิ่มขึ้น วันนี้เรามีวิธีคิดง่ายๆ ที่จะให้คุณสามารถคาดการณ์ล่วงหน้าว่า เป้าหมายทางการเงินของคุณต้องใช้ระยะเวลาเท่าไหร่ และต้องได้ผลตอบแทนเท่าใด ถึงจะทำเงินเพิ่มได้เป็น 2 เท่า โดยใช้กฎตัวเลข 72 มาฝากกันค่ะ
กฎตัวเลข 72
กฎตัวเลข 72 หรือ Rule of 72 เป็นสูตรการคำนวณแบบง่าย ที่ใช้ประมาณการผลตอบแทนว่าจะเพิ่มขึ้นเป็น 2 เท่า ต้องใช้ระยะเวลาเท่าใด หรือ ต้องได้ผลตอบแทนเท่าไหร่
กฎตัวเลข 72 กับการคำนวณเงินออม หรือเงินลงทุน
นาย A ฝากเงินไว้ในบัญชีเงินฝากดิจิทัล 100,000 บาท อัตราดอกเบี้ย 1.50% ต่อปี นาย A ต้องฝากเงินเป็นระยะเวลากี่ปี ถึงจะมีเงินเพิ่มเป็น 2 เท่า
สูตร : จำนวนปี (ที่เงินลงทุน หรือเงินออมจะกลายเป็น 2 เท่า) = 72 / อัตราผลตอบแทนต่อปี (%)
ดังนั้น นาย A ต้องฝากเงินไว้ (72 / 1.50) = 48 ปี ถึงจะมีเงินเพิ่มเป็น 2 เท่า
จากตัวอย่างการคำนวณ นาย A ต้องใช้เวลาถึง 48 ปี ในการฝากเงินไว้ในบัญชีเงินฝากดิจิทัล เพื่อที่จะให้เงินฝาก 100,000 บาท เพิ่มเป็น 200,000บาท (2 เท่า) แล้วหากนาย A ต้องการย่นระยะเวลาที่จะให้เงินฝากเพิ่มขึ้นเป็น 2 เท่า ให้เหลือเพียง 5 ปี นาย A ควรฝากเงิน หรือนำเงินก้อนนี้ไปลงทุนที่ได้ผลตอบแทนเท่าไหร่
สูตร : อัตราผลตอบแทน (ที่จะทำให้เงินลงทุน หรือเงินออมจะกลายเป็น 2 เท่า) = 72/ ระยะเวลาการลงทุนหรือการออม (ปี)
ดังนั้น นาย A ต้องลงทุนที่ได้ผลตอบแทน (72/5) = 14.4% ต่อปี นาย A จะใช้ระยะเวลาเพียง 5 ปี เงินลงทุนก็จะเพิ่มเป็น 2 เท่า
จากการคำนวณนี้ เมื่อเราทราบอัตราผลตอบแทน เราจะสามารถรู้ได้ว่า เราจะใช้ระยะเวลาเท่าไหร่ที่จะทำให้เงินโตขึ้นเป็น 2 เท่า ยิ่งเราได้ผลตอบแทนสูงเท่าไหร่ ระยะเวลาที่เงินจะเพิ่มขึ้นเป็น 2 เท่าก็จะน้อยลงเท่านั้นนะคะ
กฎตัวเลข 72 กับการคำนวณเงินกู้
นอกจากเราจะสามารถใช้ กฎตัวเลข 72 ประมาณการผลตอบแทนจากการลงทุน หรือการออมแล้ว เรายังสามารถนำมาใช้กับการคิดหนี้เงินกู้ได้ ดังนี้ค่ะ
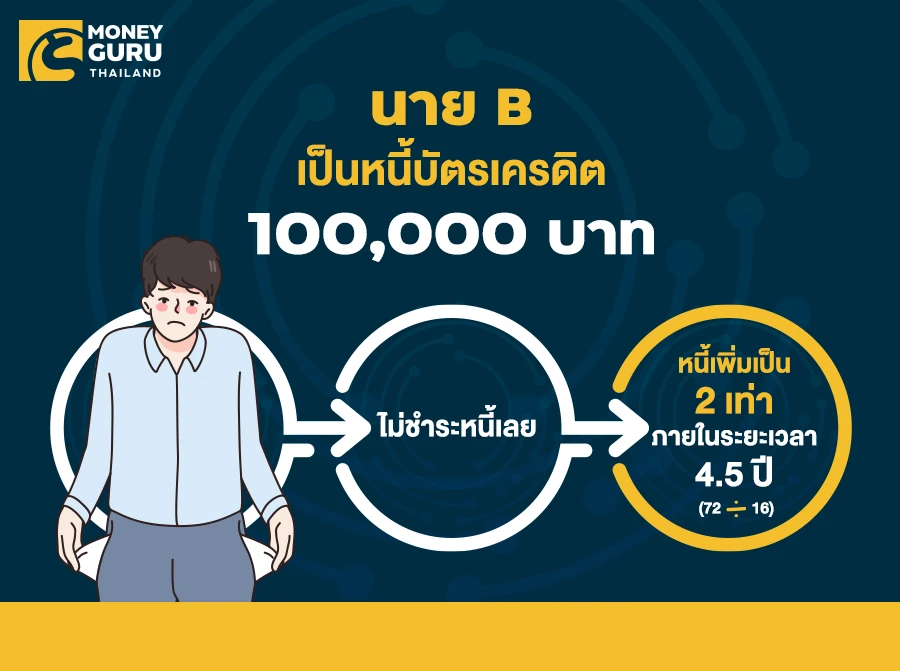
นาย B มีหนี้บัตรเครดิต 100,000 บาท ธนาคารคิดดอกเบี้ยอยู่ที่ 16% หากนาย B ไม่ชำระหนี้เลย หนี้ของนาย B จะเพิ่มขึ้นเป็น 2 เท่าในระยะเวลาเท่าใด
สูตร : จำนวนปี (ที่เงินต้นที่กดจากบัตรกดเงินสด จะเพิ่มกลายเป็น 2 เท่า) = 72 / อัตราดอกเบี้ยต่อปี (%)
ดังนั้น นาย B จะมีหนี้เพิ่มเป็น 2 เท่า หากไม่ชำระหนี้เลยภายในระยะเวลา (72/16) = 4.5 ปี
เห็นตัวเลขแบบนี้แล้ว เราควรต้องตระหนักให้ดีว่า การเก็บออม หรือการลงทุน กว่าจะได้เงินเพิ่มขึ้นเป็น 2 เท่าต้องใช้ระยะเวลาค่อนข้างยาวนาน แต่หากเป็นเงินกู้ที่เราเพิกเฉย ไม่ยอมชำระหนี้แล้ว เงินต้นจะทบขึ้นมาเป็นเท่าตัวอย่างรวดเร็ว และจะยิ่งทำให้เราติดบ่วงหนี้จนหาทางออกไม่เจอก็เป็นได้
ดังนั้น เราควรรู้จักวางแผนการเงิน ทั้งในเรื่องการออม การลงทุน โดยเลือกออม หรือลงทุนกับผลิตภัณฑ์ทางการเงินที่ให้ผลตอบแทนได้ตามที่เราต้องการ หรือควรปรึกษาผู้เชี่ยวชาญก่อนตัดสินใจลงทุน ส่วนในเรื่องของการกู้ยืมเงิน หรือใช้จ่ายบัตรเครดิตก็ควรคิดอย่างรอบคอบ ก่อหนี้เท่าที่จำเป็น และผ่อนชำระให้ตรงตามกำหนด ก็จะทำให้เราสามารถเข้าสู่เป้าหมายทางการเงินได้ตามที่วางแผนเอาไว้นะคะ



.png.webp)